

Aplicar o quadrado da oposição

Discordar da posição ou tese defendida por alguém acerca de uma determinada questão equivale a negar essa tese. Saber negar teses é um aspeto importante de qualquer discussão filosófica, dado que os filósofos passam o tempo a discordar.
Há casos em que negar teses corretamente é muito fácil, mas há outros em que isso é menos óbvio, como quando exprimimos teses filosóficas do género «Nenhuma ação humana é livre» ou «Algumas desigualdades são justas».
O quadrado da oposição, inventado por Aristóteles, ajuda-nos a negar corretamente teses como estas.
Uma negação é uma relação entre proposições. Assim, duas proposições estão envolvidas, em que cada uma é a negação da outra. Mas o que significa exatamente serem a negação uma da outra?
Significa que não podem ter o mesmo valor de verdade, isto é, se uma for verdadeira, a outra é falsa e vice-versa. Não podem, portanto, ser ambas verdadeiras nem ambas falsas.
Vejamos as proposições ou teses expressas pelas seguintes frases:
- Cristóvão Colombo viveu na ilha de Porto Santo em 1478.
- Os portugueses são tristes.
- Algumas mentiras são aceitáveis.
Como negar cada uma delas?
A primeira não levanta dificuldades (vamos designá-la 1*, para a distinguir da primeira):
1*. Cristóvão Colombo não viveu na ilha de Porto Santo em 1478.
Mas muitas pessoas têm dificuldade em negar corretamente a proposição expressa em 2, pensando que a sua negação é:
2*. Os portugueses não são tristes.
Para vermos que 2* não é a negação de 2, vamos imaginar que uns portugueses são tristes e outros não. O mais provável é que seja isto mesmo que se passa na realidade. A ser assim, então tanto as proposições expressas em 2* como em 2 são falsas. Nesse caso, elas têm o mesmo valor de verdade, pelo que não podem ser a negação uma da outra.
Isso é ainda mais claro com a negação de 3, que algumas pessoas pensam erradamente ser:
3*. Algumas mentiras não são aceitáveis.
Se for verdadeiro que só algumas mentiras são aceitáveis, o que parece razoável, então também será verdadeiro que outras não são aceitáveis. Nesse caso, tanto 3* como 3 são verdadeiras, pelo que não podem ser a negação uma da outra.
O que torna as teses 2 e 3 mais difíceis de negar do que a tese 1 é o facto de esta, diferentemente das outras duas, não ser quantificada. Uma tese ou proposição é quantificada quando inclui termos como «todos» e «alguns», ou outros equivalentes. Por exemplo, quando em 2 se fala dos portugueses, usa-se a palavra «os», para falar de todos e não de apenas de uma parte (seja grande ou pequena) deles. Por sua vez, em 3 poderíamos substituir «algumas» por «certas» sem alterar a quantificação, pois continuaríamos a referir uma parte e não todo o universo dos portugueses.
Como proceder, então, para negar corretamente proposições quantificadas? O quadrado da oposição é a melhor ferramenta lógica para isso.
O quadrado da oposição divide as proposições pela sua quantidade, havendo apenas dois tipos de quantificadores:
Universais (referem a totalidade dos indivíduos de um certo domínio ou universo): todos, os, qualquer, quaisquer.
Particulares (referem apenas uma parte e não todo o universo em causa): alguns, algum, há, certos, muitos, pelo menos um, estes, aqueles.
Mas as proposições distinguem-se também pela sua qualidade:
Afirmativas: quando atribuem uma dada qualidade ou predicado a um sujeito.
Negativas: quando negam uma dada qualidade ou predicado a um sujeito.
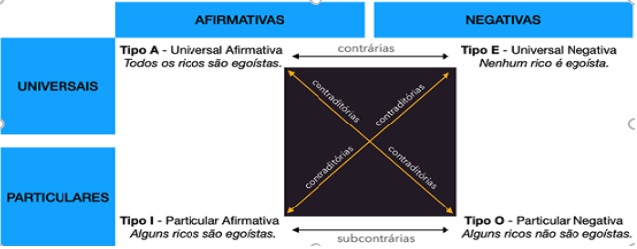
Combinando a quantidade com a qualidade, obtêm-se quatro tipos de proposições, designadas por Tipo A, Tipo E, Tipo I e Tipo O, como se pode ver no quadrado.
Assim, só as proposições contraditórias, as que têm diferente quantidade e diferente qualidade — isto é, aquelas que o quadrado apresenta como totalmente opostas —, são a negação uma da outra, pois estas são as que não podem ter o mesmo valor de verdade. Por sua vez, as contrárias (Tipo A e Tipo E), que são ambas universais, podem ser ambas falsas, mas não ambas verdadeiras. Por fim, as subcontrárias (Tipo I e Tipo O), que são ambas particulares, podem ser ambas verdadeiras, mas não ambas falsas.
É agora fácil determinar que as negações de uma tese como
Todo o conhecimento vem da experiência.
é a tese
Algum conhecimento não vem da experiência
e que a negação de uma tese como
Algumas verdades são relativas.
é a tese
Nenhuma verdade é relativa.
Em resumo:
- Saber negar proposições é um aspeto importante de qualquer discussão racional.
- Sabemos como negar proposições quantificadas aplicando o quadrado da oposição.
- A negação de uma proposição do Tipo A é outra do Tipo O, e vice-versa.
- A negação de uma proposição do Tipo E é outra do Tipo I, e vice-versa.
- A negação de uma universal é sempre uma particular, e vice-versa;
- A negação de uma afirmativa é sempre uma negativa, e vice-versa.
Temas
Ficha Técnica
- Título: Aplicar o quadrado da oposição
- Área Pedagógica: Filosofia
- Tipologia: Explicador
- Autoria: Aires de Almeida
- Produção: RTP
- Ano: 2020
- Imagem: Foto de Andrea Piacquadio no Pexels






