Conectivas proposicionais e tabelas de verdade

O que são conectivas proposicionais? Qual a importância das conectivas proposicionais? O que são tabelas de verdade? Qual a importância das tabelas de verdade?
Atentemos nas duas frases seguintes:
«Aveiro é uma cidade»
«Aveiro tem canais».
Cada uma delas exprime uma proposição simples. Com elas podemos formar outra frase e assim exprimir uma proposição complexa:
«Aveiro é uma cidade e tem canais».
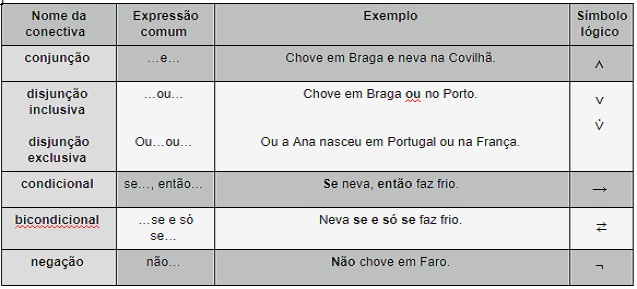
Ao juntar as duas frases iniciais numa só, usámos a palavra «e», ou seja, usámos uma conectiva. Podemos juntar as frases de diferentes maneiras, exprimindo diferentes proposições complexas. As conectivas à nossa disposição são as cinco apresentadas no quadro seguinte (que inclui, na coluna final, os respetivos símbolos lógicos):
Note-se que a negação é uma conectiva diferente das outras, pois ela não serve para unir proposições. Contudo, a negação é um operador verofuncional, como as restantes. Isso significa que dela depende o valor de verdade das proposições em que ocorre. Para se compreender o carácter verofuncional das conectivas, imagine-se que a Rita recebeu dois convites, um para ir ao cinema e o outro para ir ao teatro. Ela escolheu apenas ir ao teatro. Nesse caso, a frase
«A Rita foi ao cinema ou ao teatro»
exprime uma proposição verdadeira. Por sua vez, a frase
«A Rita foi ao cinema e ao teatro»
exprime uma proposição falsa. Mas a única diferença nas duas frases é o uso de conectivas diferentes: a disjunção na primeira e a conjunção na segunda. O valor de verdade depende, pois, das conectivas usadas. Daí elas serem verofuncionais, o que as torna especialmente importantes. Saber em que condições certas proposições são verdadeiras ou falsas, implica saber como operam as conectivas.
As tabelas de verdade mostram-nos precisamente como operam as conectivas, ajudando-nos a determinar se uma dada proposição complexa é verdadeira ou falsa, e em que condições. Essas tabelas são formas simples de especificar as condições de verdade de qualquer proposição que envolva conectivas, mostrando todas as circunstâncias possíveis e também em quais delas a proposição é verdadeira (ou falsa).
Mas como se constrói uma tabela? Tomemos como exemplo a proposição expressa pela frase:
«A Rita foi ao cinema e ao teatro»
que é formada pela conjunção das duas frases:
«A Rita foi ao cinema»
«A Rita foi ao teatro».
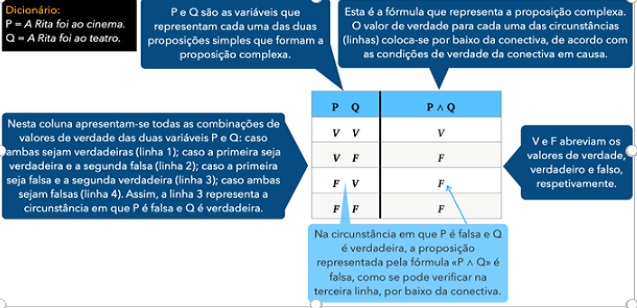
Para não se estar sempre a repetir as mesmas frases, é mais prático substituir cada uma delas por letras. Assim, a letra P pode representar a proposição simples «A Rita foi ao cinema» e Q «A Rita foi ao teatro». É preciso uma espécie de dicionário para estabelecer o que P e Q significam, uma vez que tais letras podem servir para representar qualquer outra proposição simples. Daí serem chamadas «variáveis proposicionais». As conectivas, por sua vez, têm um símbolo fixo, conforme o quadro anterior, pois elas são constantes lógicas. Usando estas convenções, ficamos com a fórmula
P ⋀ Q
que, graças ao dicionário, é fácil de interpretar. Qualquer proposição complexa pode, de resto, ser representada por uma fórmula que reproduza a sua forma lógica. Numa fórmula bem formada, uma variável só pode estar ligada a outra por meio de uma constante (ou conectiva), excetuando a negação.
A tabela de verdade seguinte mostra-nos, então, as condições de verdade da proposição complexa representada pela fórmula anterior.
Em resumo:
- As conectivas proposicionais são verofuncionais, isto, é determinam o valor de verdade das proposições em que ocorrem.
- Há cinco conectivas proposicionais: negação, conjunção, disjunção (inclusiva e exclusiva), condicional e bicondicional.
- As tabelas de verdade mostram-nos em que condições as proposições que incluem conectivas são verdadeiras ou falsas.
- Uma proposição altera o seu valor de verdade quando é negada.
- Uma conjunção só é verdadeira quando as proposições que a constituem são verdadeiras.
- Uma disjunção só é falsa quando as proposições que a constituem são falsas. No caso da disjunção exclusiva, só é falsa quando as proposições que a constituem têm diferente valor de verdade.
- Uma condicional só é falsa quando a proposição que antecede a “→” (chamada antecedente) é verdadeira e a vem depois da “→” (chamada consequente) é falsa.
- Uma bicondicional só é verdadeira quando ambas as proposições que a constituem têm o mesmo valor de verdade.
Temas
Ficha Técnica
- Título: Conectivas proposicionais e tabelas de verdade
- Área Pedagógica: Filosofia
- Tipologia: Explicador
- Autoria: Aires de Almeida
- Produção: RTP
- Ano: 2020
- Imagem: Foto de Klaus Nielsen no Pexels