Formas de inferência válida e falácias formais

O que são formas de inferência válida?  Exemplos de formas de inferência válida. O que são falácias formais? Exemplos de falácias formais.

Há inferências válidas e inválidas, pois umas vezes raciocinamos corretamente e outras incorretamente. A validade de muitas inferências depende apenas da sua forma ou estrutura, sendo o conteúdo irrelevante. As formas de inferência válida são aqueles padrões ou “moldes” de raciocínio que nos impedem de chegar a conclusões falsas a partir de premissas verdadeiras. Há inúmeras inferências, acerca dos mais diversos assuntos, que obedecem ao mesmo padrão ou forma. Se a forma for válida, então a inferência será também válida, seja qual for o seu conteúdo.

Eis três inferências diferentes que obedecem à mesma forma:

Se Gerty Cori usava auscultoscópio, então era asclépia.

Mas Gerty Cori não era asclépia.

Logo, Gerty Cori não usava auscultoscópio.

Se o Paulo ficasse zangado, deixava de falar comigo.

Mas ele não deixou de falar comigo.

Logo, o Paulo não ficou zangado.

Se a vida tem sentido, então Deus existe.

Mas Deus não existe.

Logo, a vida não tem sentido. 

Assim, se soubermos que algum deles é válido, ficamos a saber que os outros também o serão. Para apurar isso não precisamos sequer de saber quem foi Gerty Cori, assim como não precisamos de saber o que é uma asclépia e um auscultoscópio, ou mesmo de que Paulo estamos a falar e se é verdade ou não que Deus existe. Dado que todos eles partilham a forma lógica

Se A, então B

Não B

Logo, não A

basta verificar que tal forma torna impossível que as premissas sejam verdadeiras e a conclusão falsa, simultaneamente: se as premissas forem verdadeiras, não há como a conclusão ser falsa. Esta é uma forma de inferência válida muito comum e é conhecida pelo nome latino Modus tollens: tome-se uma condicional (Se A, então B); se negarmos a sua consequente (não B), podemos inferir, ou concluir, que a sua antecedente é falsa (não A).

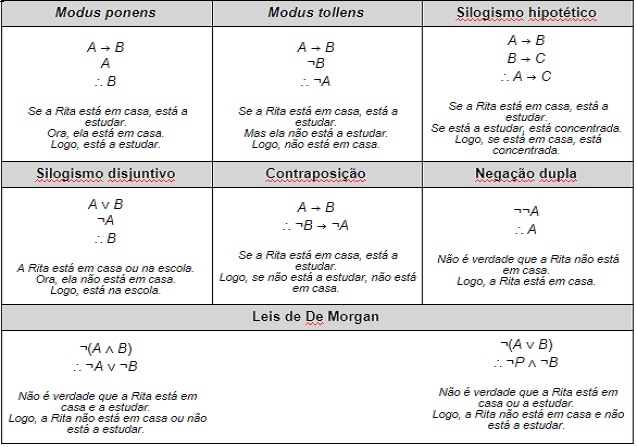
O quadro seguinte apresenta algumas das formas de inferência válida mais comuns.

É preciso ter cuidado para não confundir algumas destas formas com outras parecidas, mas que são inválidas e, portanto, enganadoras. Por parecerem ter formas válidas sem o terem, diz-se que são falácias formais. Há duas falácias formais muito comuns: a falácia da afirmação da consequente e a falácia da negação da antecedente. Eis um exemplo da falácia formal da afirmação da consequente:

Se a Rita estiver em casa, então está a estudar.

Ora, a Rita está a estudar.

Logo, está em casa.

Esta forma não nos impede de ter, simultaneamente, premissas verdadeiras e conclusão falsa, pelo que ela não é de confiança. É uma forma inválida, apesar de parecer válida, por ser parecida à forma Modus ponnens. Contudo, o que se verifica numa das premissas do Modus ponnens é a afirmação da antecedente da condicional que ocorre na outra premissa, ao passo que, na falácia da afirmação da consequente, uma das premissas é a afirmação da consequente da condicional que ocorre na outra premissa.

Para tornar mais clara a invalidade do argumento anterior, atente-se noutro argumento  com a mesma forma:

Se Adele for portuguesa, então é europeia.   [premissa verdadeira]

Ora, Adele é europeia.   [premissa verdadeira]

Logo, Adele é portuguesa.   [conclusão falsa]

Outra falácia formal recorrente é a da negação da antecedente, cuja forma se parece com o Modus tollens, como se pode comparar no quadro seguinte:

Eis um exemplo de uma falácia da negação da antecedente:

Se Adele for portuguesa, então é europeia.   [premissa verdadeira]

Ora, Adele não é portuguesa.   [premissa verdadeira]

Logo, Adele não é europeia.   [conclusão falsa]

Veja Também

Falácias informais (parte 1)